
SCIENCE COOKIES
Artículos de ciencia con chispas de chocolate
Órbita de transferencia de Hohmann
Publicado: 30/12/2020
Autor: Andrea Garma
La increíble emoción que un ser humano experimenta al ver fotogramas de lanzamientos espaciales, o si eres afortunado, escuchar con deleite como el motor de combustión del cohete produce la energía necesaria para despegar, reflejándose por un magnífico estruendo es algo que cambia la perspectiva en un segundo. A partir de ese momento, es casi imposible no preguntarse, y ahora… ¿Cómo llegará a su destino? ¿Qué ruta debe seguir para salir de la atmósfera? ¿Cómo trazan esa trayectoria?
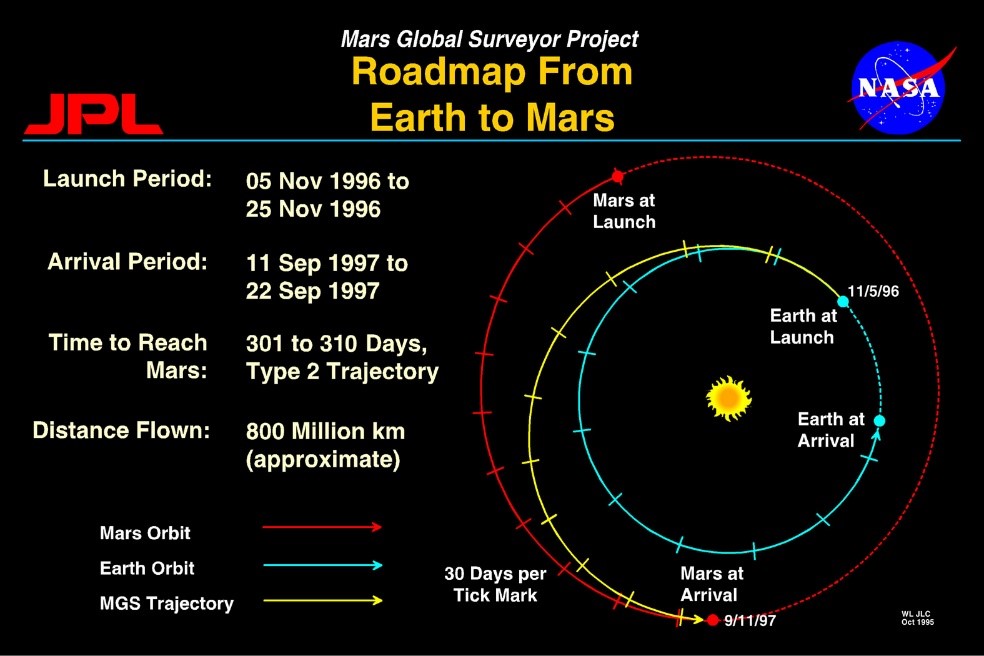
Créditos de la imagen: NASA
¿Qué es la órbita de transferencia?
Se sabe, esencialmente que para desplazarse en el espacio es necesario utilizar impulsos indirectos para poder lograr maniobras impulsivas. Sin embargo, para poder escapar de la atmósfera terrestre se requieren de rutas específicas, que no solo sean seguras y eficaces, pero también óptimas en una relación de consumo de combustible.
La órbita de transferencia es la trayectoria para seguir por parte de un objeto para desplazarse desde una órbita circular de radio “x” a una de radio “y”. La existencia de este tipo de órbitas de trayectoria, como se puede deducir, se expresa en medidas de radio.
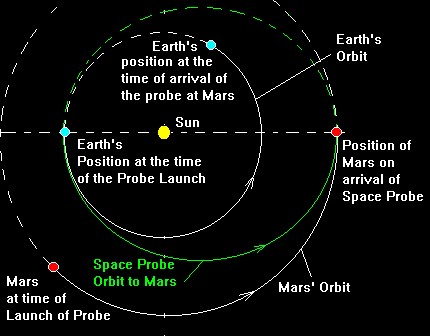
Créditos de la imagen: The Planetary Society. Planetary.org
Órbita de transferencia de Hohmann: Eficiencia
A simple vista, se podría decir que el camino más eficiente para trasladarnos de un lugar a otro es la línea recta, sin embargo, dando una mirada más de cerca a este planteamiento, nos encontramos con que las naves, al salir del campo gravitatorio de la Tierra, no siguen un M.R.U, por el contrario, se someten a las leyes gravitatorias impuestas por la gravedad solar. Lo anterior infiere un movimiento elíptico ejemplificado con aquel que sufren el resto de los cuerpos celestes de nuestro vecindario. Si se deseara llevar una ruta de línea recta, probablemente se necesitarían cantidades colosales de combustible -y costosas- para dar impulso suficiente a la nave y que esta pueda lograr la trayectoria poco eficiente.
Walter Hohman fue un ingeniero alemán que conformó un gran legado de conocimiento en el campo aeroespacial, y como se podrá concluir, es el creador de la “órbita de transferencia de Hohmann”, nacida gracias al enorme interés que el ingeniero poseía hacia los vuelos espaciales interplanetarios. Dicha órbita traza una dirección que comienza por un impulso inicial de la nave, en tierra y uno final, en la llegada a nuestro destino, el cual podría ser Marte, sí así lo deseáramos. En el camino, la nave dibuja una media elipse con el Sol, que se ubicaría como uno de sus focos y con la Tierra y Marte como vértices de la figura.
Para conformar nuestra trayectoria, se tendría en cuenta datos como la velocidad inicial y final, el impulso, los valores numéricos y las ventanas de lanzamiento.
La velocidad inicial y final se define en proporciones entre las distancias al sol, de las cuales se desprenden las siguientes expresiones:
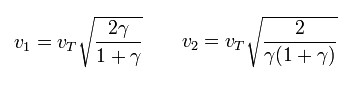
Teniendo en cuenta la atracción terrestre, la velocidad de escape y la velocidad inicial, se concluye, para cuestiones de impulso, la siguiente expresión.
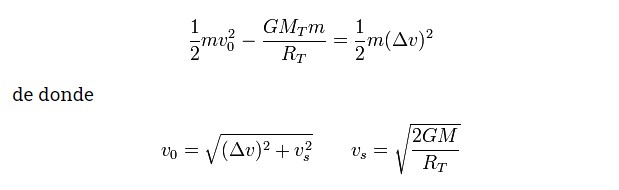
Y para materia de las ventanas de lanzamiento, la órbita de tranferencia de Hohmann funciona si las posiciones de la Tierra y Marte coinciden como puntos extremos de la elipse imaginaria, por lo cual, la posición ideal de lanzamiento se daría una vez cada 781 días.
Esperamos que este artículo te haya podido explicar un poco mejor el como viajar económicamente desde nuestro hogar hasta Marte. ¡Sigue alimentando tu cerebro con más Galletas Científicas!
Referencias
http://laplace.us.es/wiki/index.php/%C3%93rbita_de_transferencia
Moreno Vega, V., & Aeyels, D. (2005). La transferencia de Hohmann y la propiedad de consumo equivalente de combustible. Universidad, Ciencia y Tecnología, 9(33), 11-16.





